Guiding Tenets

Epistemological obstacles (EOs) are necessary challenges in a student's mathematical development that persist even in the face of research-based instruction. They are learning challenges that cannot be resolved within a single lesson, or even a unit, or an entire course. Resolving EOs requires a structural change in the way one logically reasons. To read more about EOs, click the link below.

Because EOs are necessary challenges for mathematical development, it is essential that instructors facilitate instructional interactions that elicit students experience of them. An instructor's ability to notice EOs during classroom activity is fundamental to their success in eliciting students' experience of those EOs.

The Proofs Project seeks to support instructors in addressing EOs head-on. Traditional instructional approaches often use prescibed procedures to mitigate students' learning struggles. For example, proof by mathematical induction might be taught as a three step process that students must carryout: (1) prove the base case, (2) assume the inductive assumption, and (3) prove the inductive step. However, students' experience of these challenges is fundamental to their ability to develop more robust ways of reasoning, or logical structures. The logical structures we wish for them to develop must therefore inform the instructional practices we employ. The figure below captures The Proofs Project's instructional approach.

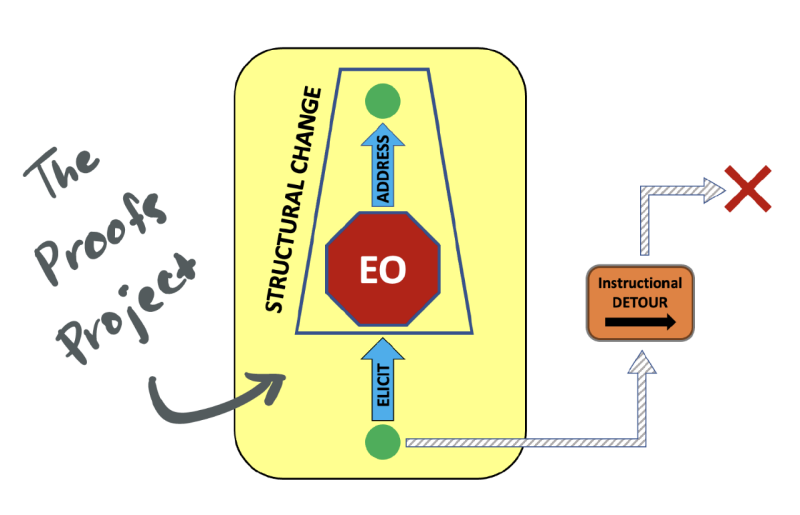
We have designed instructional modules detailing EOs in the research literature complete with examples of an instructor eliciting and addressing those EOs in an actual introductory proofs classroom. Please click below to check them out.

Establishing classroom norms and heuristics for mathematical activity are essential for scaffolding students' effective and meaningful engagement in instructional interactions surrounding research-based tasks. 

Classroom Norms

Learning is an inherently social process. Following Yackel & Cobb (1996), we distinguish two types of norms: social and sociomathematical norms. Whereas social norms are agreed about standards for what is acceptable and expected within a particular group or setting (e.g. the classroom), sociomathematical norms are standards specific to mathematical activity--they guide how mathematics is created, communicated, justified, and understood.

Norms within a classroom setting are not dictated by the teacher. While the teacher might suggest a few norms as a starting point on the first day of class, norms ultimately emerge through instructional interactions and negotations by the classroom community, itself (i.e. teachers and students). Moreover, norms must be continually reinforced and enacted in the classroom to truly become established. Please visit our classroom norms module to read more.

Heuristics

Whereas classroom norms set standards for instructional interactions, heuristics are general strategies for solving a variety of mathematical problems across contexts. An example of a commonly used heuristic is "draw a picture." Heuristics are important tools for supporting mathematical reasoning and should be integrated into introductory proof classrooms' mathematical practices. Please visit our heuristics module for illustrated examples of heuristics that are specific to proving.

Reference: Cobb, P., Stephan, M., McClain, K., & Gravemeijer, K. (2001). Participating in classroom mathematical practices. The journal of the Learning Sciences, 10(1-2), 113-163.

The Proofs Project's research-based instructional approach leverages students' existing ways of operating to support their development of logical structures necessary for robust reasoning in advanced mathematics. Recall that epistemological obstacles (EOs) are necessary challenges in students' learning that persist even in the face of research-based instruction. EOs cannot be simply removed or replaced in the context of one task, one lesson, or even one unit. Instead, they require a cognitive structural change in students' ways of operating (i.e. their existing logical structuring of their mathematical reasoning). 

We aim to support instructors to facilitate instructional interactions that:

1. Bring forth and perturb stduents current ways of operating, and
2. Provide an intellectual need for students to adapt their ways of operating.

Guershon Harel (2008) defines intellectual need as a learner's subjective need to address a challenge by learning something new. Because this need is subjective, it is essential that the instructional tasks that form the basis of classroom interactions have multiple access points. That is, they should be designed to ensure that students with different ways of operating have equitable opportunities to engage with the problem in a way that promotes further development of their existing logical structures.  

An Example of a Key Logical Structure for Proving: Logical Implication

Students' ways of operating with logical implications has been shown to significantly impact their experiences and challenges in introductory proofs courses (Norton et al., 2025). Therefore, students' treatment of logical implication is an example of a key logical structure that instructors should attend to developing within instructional interactions. Click below to read more about how students' cognitive structuring of logical implication, an an action versus an object, impacts their learning experiences.

References:

1. Harel, G. 2008. What is mathematics? A pedagogical answer to a philosophical question. In R. B. Gold.
2. Norton, A., Antonides, J., Arnold, R., & Kokushkin, V. (2025). Logical implications as mathematical objects: Characterizing epistemological obstacles experienced in introductory proofs courses. The Journal of Mathematical Behavior, 79, 101253.