Heuristics

How many instructors have been asked by their students, "do I need to say this?" or "how do I know what to say next?". If instructors simply present the final written product of a proof, students may be able to follow along and yet still remain unsure as to how to produce such a proof on their own. Students need opportunities to struggle, in necessary and productive ways, with developing and formalizing proofs. In particular, they need opportunities to think about the necessary components of a proof, how to structure it logically, and how to distinguish the work that goes into developing a proof that should not be included in the final written product. These experiences are essential for helping students buy into and adopt proof-writing norms (norms that experienced mathematicians often take for granted).

To help provide students with these opportunities for critical thinking and reflection, we encourage students to engage in "rough draft" thinking (Jansen, 2020) by creating space, alongside their formal written proof, for thinking about and writing down important, necessary details (i.e., "solving for the proof"). We have found that this separation provides students with opportunities to make sense of the logical framing of a proof before formalizing these details into a written product that uses normative language of logic and proof.

To demonstrate how this might be done, consider the task shown below.

The instructor divides her notes into two columns: one column for solving for the proof and one column for writing the formal proof. The video below shows the instructor leading whole-class discussion after students have had a chance to work on the task in groups.

An Important Distinction Between an Introductory Proofs Course and the Courses that Precede it

In math courses preceding introductory proofs, emphasis is primarily placed on students showing their work, i.e. the process by which they arrive at a solution. The solution process, however, does not constitute a normative proof. The proof instead presents the solution and then shows that it does indeed work. The order in which statements are presented in the proof is often the reverse of the order in which they are derived in the solution process.

Tasks like the one below can be a first step in helping students make distinctions between "solving for a proof" and "presenting a proof."

Inviting students to analyze the validity of two "proofs" (one that solves for the proof versus one that presents the proof) offers them opportunities to develop the intellectual need for separating solving for a proof and writing the proof. This next video shows the whole-class discussion immediately following students' group work on the above task.

One of the most difficult tasks inherent in proving is deriving a chain of inferences that allows the conclusion to be deduced from the given hypotheses. This process is what famous scientist and philosopher Charles Peirce calls abduction. Specifically, he says “[a]bduction is the process of forming explanatory hypotheses. It is the only logical operation which introduces any new idea” (Peirce, 5.172).

In Rachel Arnold's philosophy of teaching statement, she stresses the importance of using desired conclusions to motivate students' exploration of solution paths toward those conclusions. Without this approach, she asks, "how can one make good choices from among many potentially relevant givens and their implications?"

Prior to introductory proofs, students are trained to begin problems by writing down the given information. In constructing a proof, however, beginning by arbitrarily piecing together hypotheses doesn't usually lead to a successful outcome. Beginning instead by understanding the desired conclusion should help reveal which aspects of the hypotheses are relevant. 

There is a difference between understanding the conclusion and assuming it. 

It is a common practice for introductory proofs instructors to warn students against assuming the conclusion. This warning may lead to the undesirable result of students avoiding the conclusion altogether when solving for the proof. Instructors must be careful to emphasize that understanding the conclusion is essential to developing a proof. The conclusion should actually be the first place that students look when situating themselves with the statement they are to prove.

In the next video, the teacher explicitly reinforces understanding the conclusion first before determining how the hypotheses are relevant.

To see this enacted within the context of a specific example, consider the task shown below. 

After allowing time for students to work in groups, it emerged that many were struggling with statement 3 in particular. The instructor briefly brought the class back together to remind them to start by understanding the conclusion. See the video below.

Students then went back into groups to continue working. This time, the instructor observed many students making progress on the problem. Afterward, in the next video, the instructor went over the process of solving for the proof with the class as a whole.

Reference:

Peirce, C. S. Collected Papers of Charles Sanders Peirce, edited by C. Hartshorne, P. Weiss, and A. Burks, 1931–1958, Cambridge MA: Harvard University Press.

As mathematical statements become increasingly complex and/or abstract, it is important for students to have tools for visualizing them. Visualizations play a key role in students' sense-making of mathematical symbols. Examples of various visual tools that instructors can and should equip their students with are:

1. Euler Diagrams
2. Geometric/graphical representations
3. Schematic Diagrams

Visualizing Mathematical Logic with Euler Diagrams

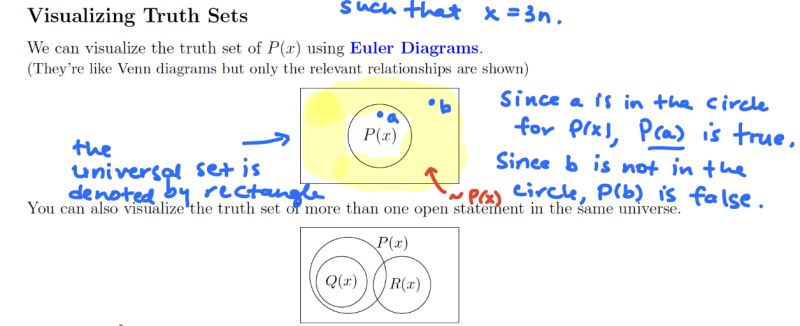
Hub & Dawkins (2018) have found that set-based reasoning may support students' understanding of mathematical logic, especially across contexts.  Euler diagrams allow students to visualize logic via truth sets so that might leverage spatial reasoning to make sense of mathematical statements. 

This next video shows an instructor introducing students to Euler diagrams and how they might offer information about whether a statement is true or false. Her instructional task and the notes that she produces are pictured above.

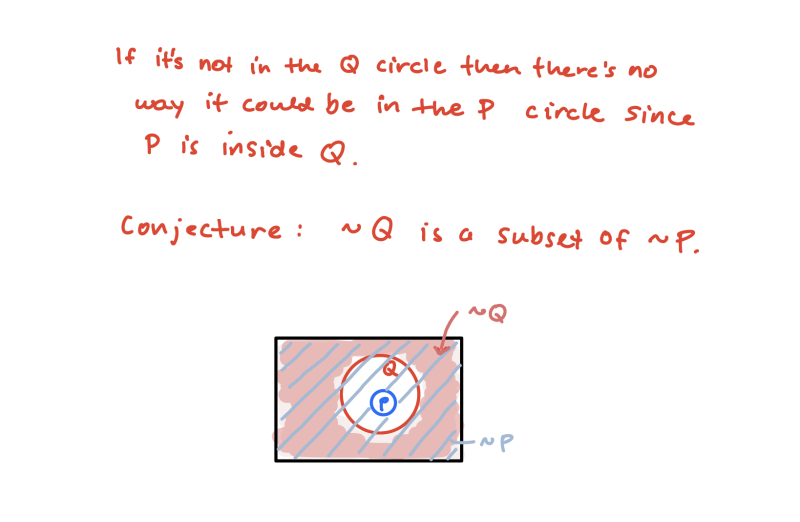
The video below occurs two class meetings after the one above. After working on a group task, students have conjectured that a logical implication and its contrapositive are logically equivalent. The class is now discussing how they might determine whether this is true. One student articulates that it must be true via spatial reasoning and his understanding of the connection between the Euler diagram and mathematical logic. An image of the notes produced in this interaction is below the video.

Interpreting Statements Through Geometric Meaning

Instructors can use tasks like the one below to explicitly demonstrate how using geometric meaning of algebraic expressions can help build intuition.

The video below shows the instructor introducing this task and then facilitating the follow-up classroom discussion after students had worked on the problem in groups. When a student offers a counterexample to the statement, the instructor prompts students to check whether it works. Anticipating that most students verify the counterexample by subsituting the values for a, b, and c, she encourages the class to conceptualize the inequalities geometrically, as restrictions on distances between two points.  

Using Schematic Diagrams to Understand a Conjecture

Schematic diagrams can offer students a way to visualize complex mathematical statements. For example, while students might be familiar with graphing functions in the xy-plane, they may be less equipped with tools to visualize abstract functions. Consider the following task:

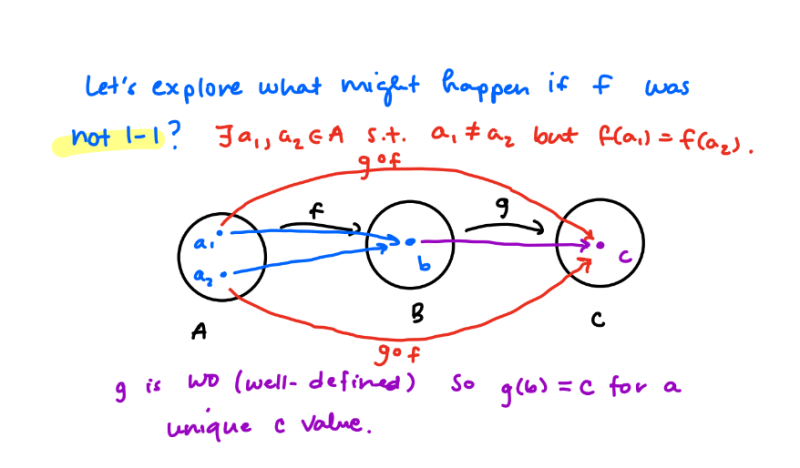
After working in groups, students offered several conjectures. In response to question 1, one student suggested that f must also be 1-1. To understand whether this conjecture was true or false, the instructor drew a schematic diagram shown below.

The video below shows, via whole-class discussion, how this schematic diagram supports determining that the conjecture is indeed true and lays the framework for its proof.