Quantification

"... finding something out about understanding quantification, how it is learned, and what we as teachers can do to help might contribute to the goal of improving all students' understanding of advanced mathematical ideas."
-- Dubinksy, Elterman, & Gong (1988)
Quantification of a mathematical statement specifies the scope of mathematical objects over which the statement applies. In mathematical logic, there are two common ways to quantify a statement, P(x):
- Universally: "For all x, P(x)."
- Existentially: "There exists an x such that P(x)."
The quantification of a mathematical statement determines the scope of its claim and therefore affects the logic required for proving it. Generally, the proof of a "for all" statement demands more than the proof of an existence statement.
Identified Epistemological Obstacles
In the negation of a statement, its quantification is changed (from "for all" to "there exists" or vice versa). Therefore, the logical framework for proving the negation is different from proving the original statement. For example, if the original statement claimed "all prime numbers are odd," its negation would simply claim "there exists a prime number that is even." In this case, to prove the negation, providing the example of 2 would suffice.
Quantification of the negation can present an obstacle in instructional interactions, especially in generating proofs by contradiction. Research demonstrates that students often state the opposite of a statement as its negation (Epp, 2003). For example, consider the implication,
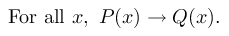
Students might state the negation as:
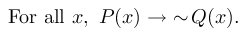
However, unlike the correct negation, this statement can be (vacuously) true without disproving the original implication. Here, we provide tasks and video-based examples for eliciting the EO and addressing it.
Counterexample Versus Negation
The negation of a universally quantified statement is the assertion that "there exists a counterexample." As you will see below, while students seem comfortable with producing a counterexample, they experience difficulty in articulating the precise negation of a statement. Some students also conflate the task prompt `"find the negation of the statement" with "prove the negation is false." Struggles with quantification contribute to the apparent cognitive gap between counterexample and negation.
To elicit this potential obstacle, the instructor introduces a task wherein students must negate the following statement:
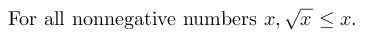
She frames the task as finding the "complementary" statement--the statement with opposite truth value. When a student introduces a counterexample to the original statement, discussion turns to quantification. One student suggests that we must "invert" the quantification of x, replacing the beginning of the original statement with "for no nonnegative numbers x." For this student, the inversion of "for all" is "none" (not "there exists"). See the EO regarding treating the negation as the "opposite" for more about this common phenomenon.
The video below captures the Hexagon group engaging with this task. They struggle to distinguish between proving P is false and articulating the statement that is equivalent to P being false. Students feel unsure of their response (which simply provides the counterexample of x = 1/4) and anticipate coming back together as a class to discuss the task.
To address issues of quantification in negating mathematical statements, the instructor introduced a new task (shown below), for students to solve in their groups.
The following video shows how the instructor launched the task and how students responded during whole-class discussion after working in groups. Note that whole-class discussion focuses on the shift in quantification between the original statement and its negation. These shifts in quantification are also notated in the task image (above): "for some," "there exists," "for all," and "there is no...".
The next video shows the Hexagon group's discussion. Notice that they are now able to attend to quantification when stating the negation. Although, a student still articulates negating the statement as "disproving" the claim.
Below, the Rectangle group also attends carefully to quantification of the negation. Note that one student still questions whether the negation should demonstrate a specific value (i.e. a counterexample).
Whereas the discussion above took place at the start of the semester, the following discussion took place two months later, in the middle of the semester. Students are now working in the context of multiply-quantified statements, where negation becomes even more complicated.
Students were asked to evaluate statements about points related to a circle, S, with radius 5 (see image below). Class discussion (illustrated in the following video) centered on the negation of statements 1(f) and 1(g).
To assist students in negating these multiply quantified statements, the instructor employs the method of negation called negation by recursion (Dubinksy, Elterman, & Gong, 1988). Parsing the statement 1(g) into its general structure of "for all points a in S, *something* is true" seems to help students attend more carefully to the negation's shift in quantification. By suppressing the remaining statement, "there is a point b on S such that d(a,b) = 7," as a single proposition, statement 1(g) now follows a simpler, more accessible form ``for all x, P(x)."
Attending to quantification can become especially problematic when quantifiers are hidden (Shipman, 2016). For example, consider the statement:
If x is a multiple of 6, then x is a multiple of 3.
This statement has a hidden universal quantification and we read it implicitly as:
For all integers x, if x is a multiple of 6, then x is a multiple of 3.
Overlooking hidden quantifiers can result in logical fallacies, especially in the case of proof by contradiction (like the task pictured below). Students need practice interpreting the logic of statements that are both explicitly and hiddenly quantified.
In the image shown below, there are several examples of existence statements, some of which have hidden quantification. For example, in the matrix example, the statement is actually a statement of existence--the existence of an inverse matrix for the given matrix, A.

Tasks and examples like these can elicit discussion about hidden quantifiers so that students might begin to attend to quantification and its role in making meaning of logical statements. In the video below, the instructor asks students to explain why the matrix statement above is an existence statement. Following the video, we share the Triangle group discussion.
At first, the Triangle group focuses on computing the inverse of the matrix using rules that they tried to recall from Linear Algebra. Then, one student refocuses the group on the task of figuring out how the given statement is an existential statement.
Likewise, and as shown in the image below, "for all" statements can be expressed in various ways, some of which might obscure the universal quantification. The following video illustrates group discussion, from the Triangle group, about the examples shown in the image. The group begins to address hidden quantification by making explicit how each example statement is quantified and how this quantification effects its meaning.

Logical statements containing multiple quantifiers, or multiply quantified statements, exacerbate students’ struggles with quantification. For example, Dawkins and Roh (2020) found that students tend to read multiply quantified statements semantically, applying their contextual knowledge to make sense of the formal statements, thereby neglecting the syntax of the statement and the order of the quantifiers in particular (Piatek-Jimenez, 2010). In our framing, such EOs should be deliberately evoked and carefully addressed over time.
The statements shown in the image below contain two or more variables and may be used to offer students a first look at multiply quantified statements.
Instructors might elicit challenges associated with the order of quantification by asking whether it matters which variable is quantified first. In the video that follows, students in the Triangle group first spend time trying to understand what this question is asking, which might indicate they had never considered order of quantification to be an issue. Then, they begin to consider how the order of quantification might change the meaning of a statement.
Following the group work, a classroom discussion ensued. During discussion, a student suggested that the order of quantification might affect dependency between two variables. For example, if we say, "there's an x such that for every y..." this might imply the same value of x has to work for all y. On the other hand, if we say, "there is an x for every y" this might imply that different x's can work for every y.
Note that in explaining her reasoning, the student chose to move the location of the "such that" in the statement instead of rearranging the order in which each variable was introduced. "There is an x for every y such that..." is equivalent to "For every y, there is an x such that...". Inviting students to compare and contrast how the position of the "such that" changes the corresponding mathematical logic is also an important task in which to engage students.
To support students as they address challenges associated with the order of quantification, the instructor used an instructional task that students could visualize. The task involved distances between points related to a given circle, S, of radius 5 (see the image below).
After the instructor introduced the task, students began working in their groups. The following video comes from the Triangle group. Students in that group are discussing scenario 1(e): "For all points a on S, there exists a b in S such that d(a,b) = 2." They question whether this statement implies that the same point b must work for all points a. They seem to be making a logical distinction between the language "for every point a" and "for all points a." To them, the former suggests they might choose a new value of b each time, and the latter might not allow for the choice a new value of b each and every time.
We can see similar discussion among the Rectangle group, as they solve a similar task involving multiple quantifiers within an algebraic equation (see image below). In evaluating the third statement in this task, one of the students draws a diagram to keep track of the various dependencies between variables. You can read more about the importance of encouraging this heuristic (using visuals to build intuition) in the Heuristic Module here.
Students often confuse the negation of a statement with its opposite. For example, they might say the negation of "every x has property P" is "every x does not have property P." In the context of implication, students might state the negation of "P implies Q" as "P implies ~Q." This apparent conflation can be an issue of quantification. Negation of a universally quantified statement requires the existence of a single counterexample.
In the following video, the instructor asks for the negation of a multiply-quantified statement. To simplify the question, the instructor encourages the students to treat the conclusion of the statement (which contains the second quantified variable) as "stuff that happens." Still, a student suggests that the negation of the statement would the be the statement with the same quantification but the opposite conclusion. Although another student offers a correction with which the first student agrees, we can see persistent challenges associated with negating quantified statements and the tendency for students to think of a statement's negation as its opposite.
To address continuing challenges associated with quantification and negation, the instructor used a visual task involving a circle, S, of radius 5. Students worked in groups to answer related questions, such as finding the negation of the statement, "there is a point b on S such that for any point a inside S, d(a,b) = 5." In the following video, we hear two students discussing issues of quantification related to stating the correct negation. Notice that they make sense of the original statement by relying on the drawing, affirming the support offered by visualization. Also notice that one of the students initially assumes that the negation must be an existence statement because "we just have to find one counterexample to show it's not true."
Annotated bibliography