Joseph Wells

460 McBryde Hall, Virginia Tech
225 Stanger Street
Blacksburg, VA 24061-1026
What things do I think about? I'm generally interested in the interplay between groups and geometry, especially in the realm of discrete subgroups of Lie groups and the corresponding homogeneous spaces.
Okay. What does that mean? Well, here's a toy example. Given any pair of integers m and n, we can define a function fm,n which takes points in the Cartesian plane and translates them m units right and n units up (the convention is that if m is negative, the translation is to the left, and if n is negative, then the translation is down). We'll call the entire collection of these functions ℤ2, i,e.
Now look at the unit square with vertices (0,0), (1,0), (1,1), and (0,1) (shaded in blue below). Notice that, if we apply all of the functions in ℤ2 to this blue square, then we start to tile the entire Cartesian plane.
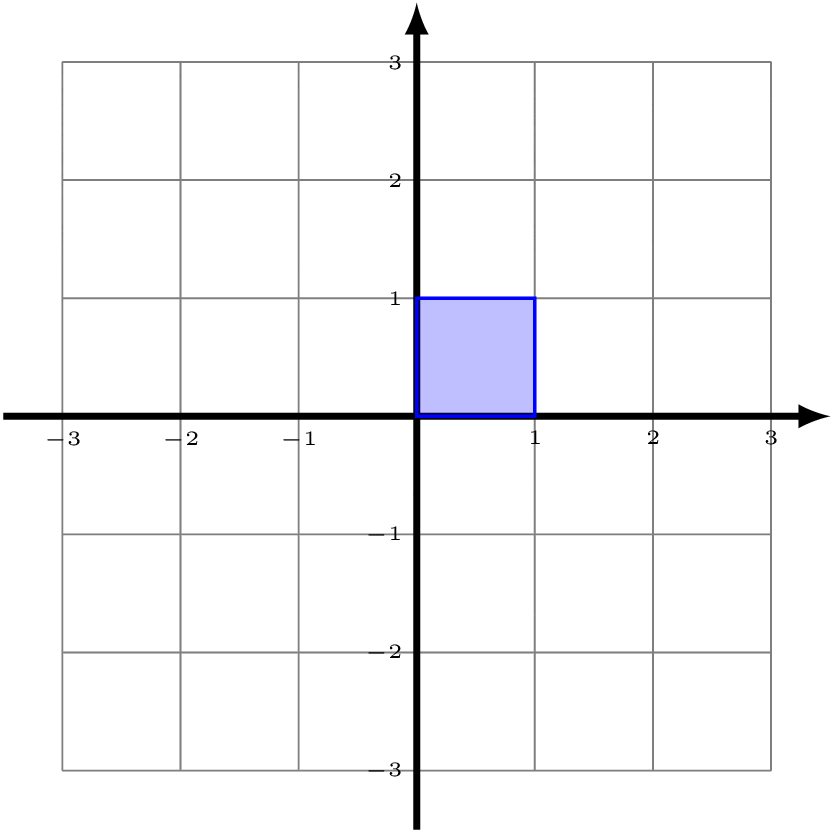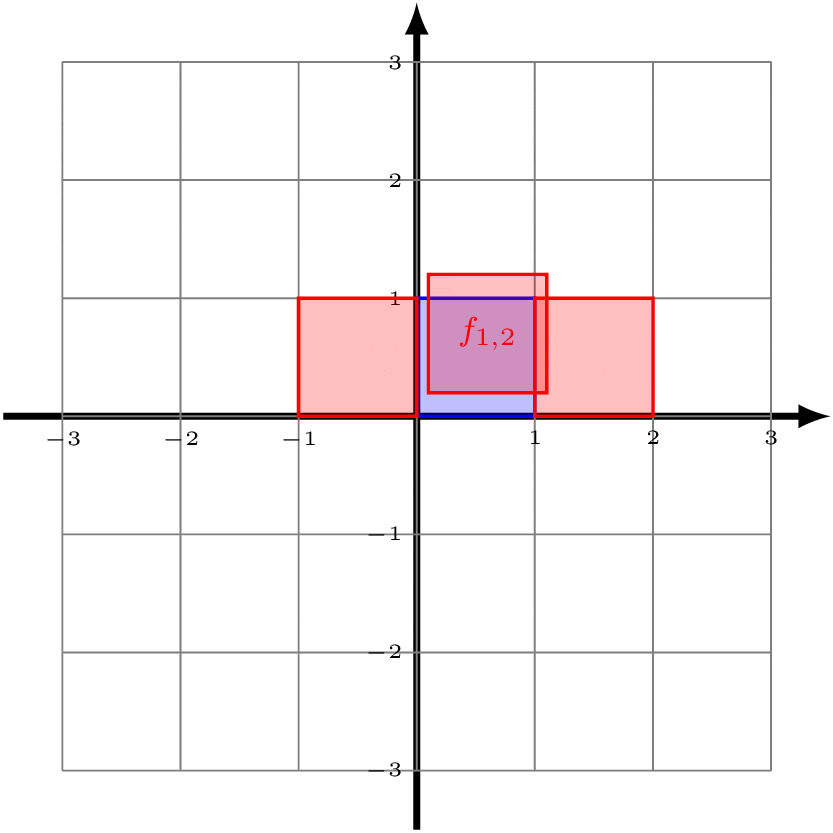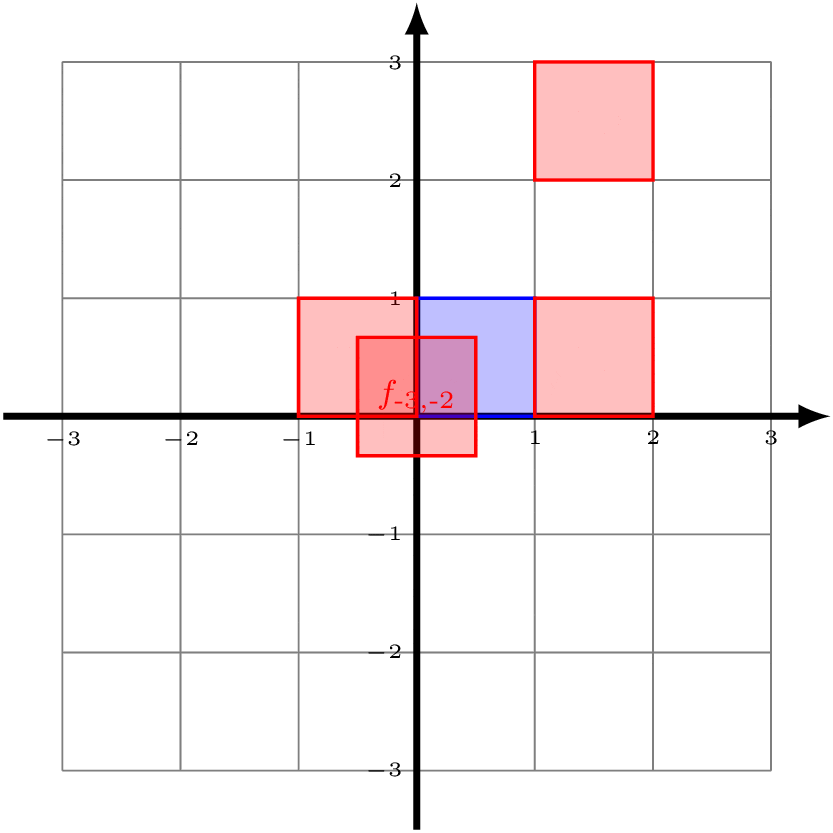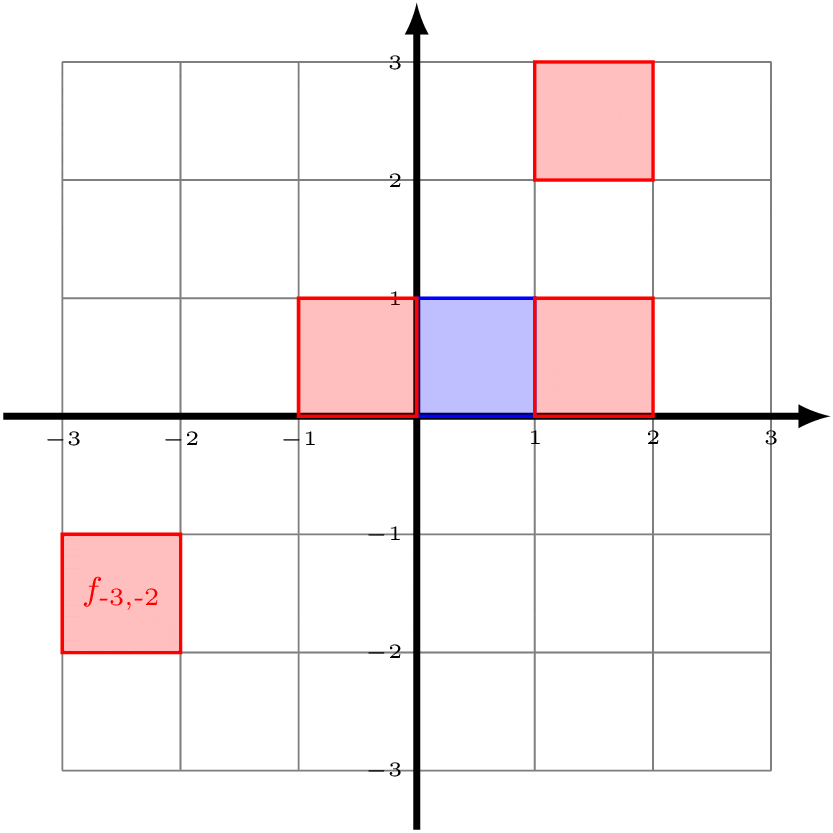
You can convince yourself that the square with side length 1 is the only rectangle that will have this property. If the bottom and top side had length 2, then there would be all sorts of overlap. Because of this, we can say that the blue square is a "fundamental domain" for ℤ2 acting on the Cartesian plane. (Note that our choice to specify those particular corners was completely arbitrary.)
Now, it turns out that the functions f1,0 and f0,1 are pretty special -- every possible function in ℤ2 can be written by just composing these two functions together a bunch of times. For example,
But these two functions are also special for a geometric reason -- the function f1,0 exactly takes the left side of the fundamental square over to the right side of the fundamental square, and the function f0,1 takes the bottom side of the fundamental square to the top side of the fundamental square.
Let's take the perspective that these functions actually tell us how to glue up our fundamental square: if one side is taken to another by either f1,0 or f0,1, then those sides get glued up. The functions f1,0 and f0,1 then result in gluing this square up into the torus T2 (the surface of a donut).
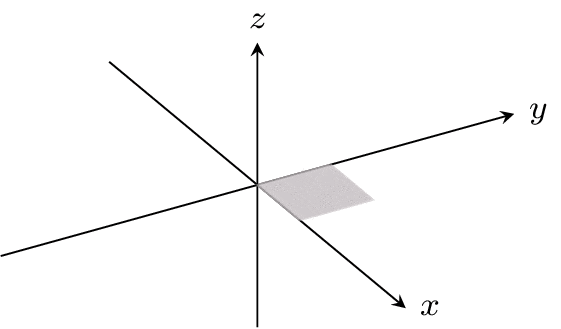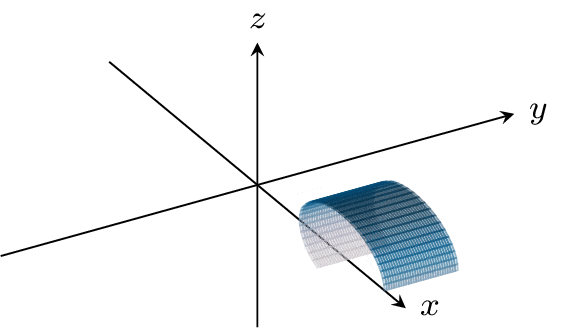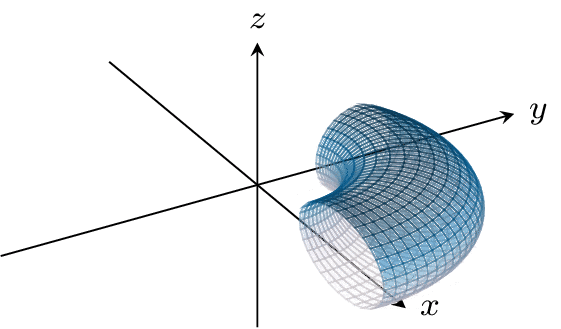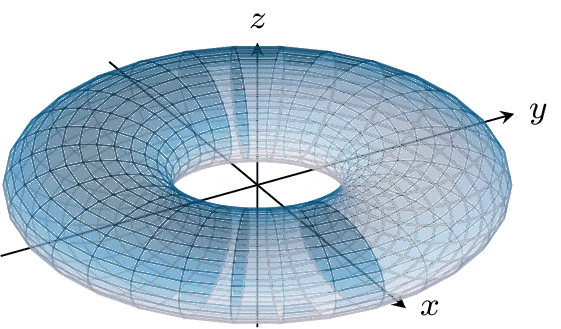
Because of this, we can say that the geometry of T2 is determined by this collection of functions ℤ2. There are many more connections between the geometric properties of T2 and the algebraic properties of ℤ2, but that's a discussion for a different time.
More generally: It's a basic exercise to prove the following things about ℤ2:
- ℤ2 is a group, where the group operation is just function composition and (fm,n)-1 = f-m,-n 2m,n
- ℤ2 is a subgroup of ℝ2 (where ℝ2 is defined analogously to ℤ2).
- Making the canonical identification of ℝ2 with ordered pairs (x,y) and the standard topology, ℝ2 inherits the structure of a Lie group, and in turn ℤ2 inherits the discrete topology.
- The group action of ℤ2 on ordered pairs (x,y) is by isometries. In other words, for the standard distance function dist, one has that dist( fm,n(x1,y1) , fm,n(x2,y2) ) = dist( (x1,y1) , (x2,y2) ).
- The group action is free.
And so, I like to think about the more general situation: Given my favorite topological space X with nice properties, the group of isometries Isom(X) is a Lie group. A discrete subgroup Γ of this isometry group is called a lattice when the fundamental polytope in X has finite volume. Modulo some technical assumptions, this fundamental polytope then glues up via a finite collection of functions in Γ and forms a particularly nice geometric object called a manifold, M, which we might write as M=Γ\X. The correspondence actually goes the other way too -- modulo some technical assumptions, every manifold I care about can be obtained from such a Γ. Because of this connection, when dimensions get too high to actually "see", we can still try to understand both Γ and M via the precise connections between the algebraic properties and the geometric properties.


